
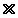

 http://www.clearlight.com/~morph/dna/dne.htm (Internet on a CD, 07/1998)
http://www.clearlight.com/~morph/dna/dne.htm (Internet on a CD, 07/1998)Go To Scientific Version

Despite their respective complexities, biological and mathematical operations have some similarities:
For the same reasons that DNA was presumably selected for living organisms as a genetic material, its stability and predictability in reactions, DNA strings can also be used to encode information for mathematical systems.
Figure 1 shows a diagram of the Hamiltonian Path problem. The objective is to find a path from start to end going through all the points only once. This problem is difficult for conventional (serial logic) computers because they must try each path one at a time. It is like having a whole bunch of keys and trying to see which fits a lock. Conventional computers are very good at math, but poor at "key into lock" problems. DNA based computers can try all the keys at the same time (massively parallel) and thus are very good at key-into-lock problems, but much slower at simple mathematical problems like multiplication. The Hamiltonian Path problem was chosen because every key-into-lock problem can be solved as a Hamiltonian Path problem.[2]
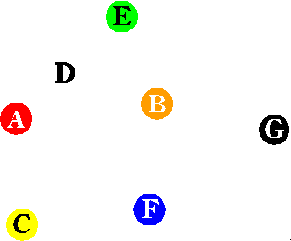
The following algorithm solves the Hamiltonian Path problem, regardless of the type of
computer used:
The key to solving the problem was using DNA to perform the five steps in the above
algorithm.
These interconnecting blocks can be used to model DNA:
![]()
DNA likes to form long double helices:

The two helices are joined by "bases", which will be represented by coloured
blocks. Each base binds only one other specific base. In our example, we will say that
each coloured block will only bind with the same colour. For example, if we only had red
blocks, they would form a long chain like this:

Any other colour will not bind with red:

Step 1: Create a unique DNA sequence for each city A through G. For each path, for example, from A to B, create a linking piece of DNA that matches the last half of A and first half of B:
![]()
In a test tube, all the different pieces of DNA will randomly link with each other,
forming paths through the graph.
Step 2: Because it is difficult to "remove" DNA from the solution, the target DNA, the DNA which started at A and ended at G was copied over and over again until the test tube contained a lot of it relative to the other random sequences. This is essentially the same as removing all the other pieces. Imagine a sock drawer which initially contains one or two coloured socks. If you put in a hundred black socks, chances are that all you will get if you reach in is black socks!
Step 3: Going by weight, the DNA sequences which were 7 "cities" long were separated from the rest. A "sieve" was used which allows smaller pieces of DNA to pass through quickly, while larger segments are slowed down. The procedure used actually allows you to isolate the pieces which are precisely 7 cities long from any shorter or longer paths.
Step 4: To ensure that the remaining sequences went through each of the cities, "sticky" pieces of DNA attached to magnets were used to separate the DNA. The magnets were used to ensure that the target DNA remained in the test tube, while the unwanted DNA was washed away. First, the magnets kept all the DNA which went through city A in the test tube, then B, then C, and D, and so on. In the end, the only DNA which remained in the tube was that which went through all seven cities.
Step 5: All that was left was to sequence the DNA, revealing the path from A to B to C to D to E to F to G.
The above procedure took approximately one week to perform. Although this particular
problem could be solved on a piece of paper in under an hour, when the number of cities is
increased to 70, the problem becomes too complex for even a supercomputer. While a DNA
computer takes much longer than a normal computer to perform each individual calculation,
it performs an enourmous number of operations at a time (massively parallel). DNA
computers also require less energy and space than normal computers. 1000 litres of water
could contain DNA with more memory than all the computers ever made, and a pound of DNA
would have more computing power than all the computers ever made [3]
DNA computing is less than two years old (November 11, 1994), and for this reason, it is too early for either great optimism of great pessimism. Early computers such as ENIAC filled entire rooms, and had to be programmed by punch cards. Since that time, computers have since become much smaller and easier to use. DNA computers will become more common for solving very complex problems; Just as DNA cloning and sequencing were once manual tasks, DNA computers will also become automated.
In addition to the direct benefits of using DNA computers for performing complex computations, some of the operations of DNA computers already have, and perceivably more will be used in molecular and biochemical research.
 |
I have complete models to describe the entire process of DNA-based computing beyond what appears on this page. If you would like to publish my model in television, print, or other media, please contact me at morph@clearlight.com |