


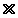

 http://www.sgi.com/grafica/texmap/index.html (Silicon Surf Promotional CD, 01/1995)
http://www.sgi.com/grafica/texmap/index.html (Silicon Surf Promotional CD, 01/1995)But texture mapping hardware can be used for many more applications than simply applying diffuse patterns to polygons.
We survey applications of texture mapping including simple texture mapping, projective textures, and image warping. We then describe texture mapping techniques for drawing anti-aliased lines, air-brushes, and anti-aliased text. Next we show how texture mapping may be used as a fundamental graphics primitive for volume rendering, environment mapping, color interpolation, contouring, and many other applications.
CR Categories and Subject Descriptors: [Computer Graphics]: Picture/Image Generation; I.3.7 [Computer Graphics]: Three-Dimensional Graphics and Realism - color, shading, shadowing, texture-mapping, line drawing, and anti-aliasing
Because texture mapping is so useful, it is being provided as a standard rendering technique both in graphics software interfaces and in computer graphics hardware[Hanrahan 90][Deering 88]. Texture mapping can therefore be used in a scene with only a modest increase in the complexity of the program that generates that scene, sometimes with little effect on scene generation time. The wide availability and high-performance of texture mapping makes it a desirable rendering technique for achieving a number of effects that are normally obtained with special purpose drawing hardware.
After a brief review of the mechanics of texture mapping, we describe a few of its standard applications. We go on to describe some novel applications of texture mapping.
In practice, the required filtering is approximated by one of several methods. One of the most popular is mipmapping[Williams 83]. Other filtering techniques may also be used [Crow 84].
There are a number of generalizations to this basic texture mapping scheme. The image to be mapped need not be two-dimensional; the sampling and filtering techniques may be applied for both one- and three-dimensional images [Peachey 85]. In the case of a three-dimensional image, a two-dimensional slice must be selected to be mapped onto an object's boundary, since the result of rendering must be two-dimensional. The image may not be stored as an array but may be procedurally generated [Peachey 85][Perlin 85]. Finally, the image may not represent color at all, but may instead describe transparency or other surface properties to be used in lighting or shading calculations [Carey 85].
Projective textures are also useful for simulating shadows. In this case, an image is constructed that represents distances from a light source to surface points nearest the light source. This image can be computed by performing Z-buffering from the light's point of view and then obtaining the resulting Z-buffer. When the scene is viewed from the eyepoint, the distance from the light source to each point on a surface is computed and compared to the corresponding value stored in the texture image. If the values are (nearly) equal, then the point is not in shadow; otherwise, it is in shadow. This technique should not use mipmapping, because filtering must be applied after the shadow comparison is performed [Reeves 87].
![]()
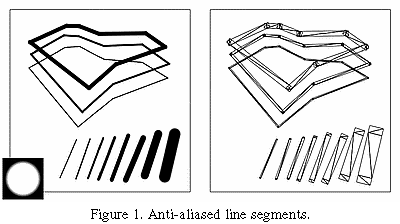
One simple use of texture mapping is to draw anti-aliased points of any width. In this case the texture image is of a filled circle with a smooth (anti-aliased) boundary. When a point is specified, it's coordinates indicate the center of a square whose width is determined by the point size. The texture coordinates at the square's corners are those corresponding to the corners of the texture image. This method has the advantage that any point shape may be accommodated simply by varying the texture image.
A similar technique can be used to draw anti-aliased, line segments of any width [Grossman 90]. The texture image is a filtered circle as used above. Instead of a line segment, a texture mapped rectangle, whose width is the desired line width, is drawn centered on and aligned with the line segment. If line segments with round ends are desired, these can be added by drawing an additional textured rectangle on each end of the line segment (Figure 1).
![]()
![]()

Antialiased characters of any size may be obtained with a single texture map simply by drawing a polygon of the desired size, but care must be taken if mipmapping is used. Normally, the smallest mipmap is 1 pixel square, so if all the characters are stored in a single texture map, the smaller mipmaps will contain a number of characters filtered together. This will generate undesirable effects when displayed characters are too small. Thus, if a single texture image is used for all characters, then each must be carefully placed in the image, and mipmaps must stop at the point where the image of a single character is reduced to 1 pixel on a side. Alternatively, each character could be placed in its own (small) texture map.
The second method uses 3D texture mapping [Drebin 92]. In this method, the volumetric data is copied into the 3D texture image. Then, slices perpendicular to the viewer are drawn. Each slice is again a texture mapped polygon, but this time the texture coordinates at the polygon's vertices determine a slice through the 3D texture image. This method requires a 3D texture mapping capability, but has the advantage that texture memory need be loaded only once no matter what the viewpoint. If the data are too numerous to fit in a single 3D image, the full volume may be rendered in multiple passes, placing only a portion of the volume data into the texture image on each pass.
A third way is to use texture mapping to implement "splatting" as described by [Westover 90][Laur 91].
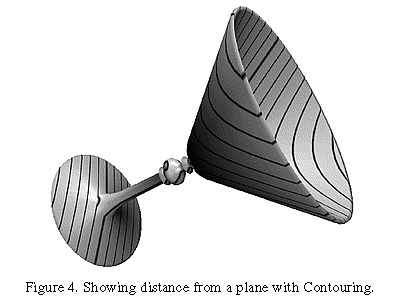
Contouring is achieved with texture mapping by first defining a one-dimensional texture image that is of constant color except at some spot along its length. Then, texture coordinates are computed for vertices of each polygon in the object to be contoured using a texture coordinate generation function. This function may calculate the distance of the vertex above some plane (Figure 4), or may depend on certain surface properties to produce, for instance, a curvature value. Modular arithmetic is used in texture coordinate interpolation to effectively cause the single linear texture image to repeat over and over. The result is lines across the polygons that comprise an object, leading to contour curves.
![]()
A two-dimensional (or even three-dimensional) texture image may be used with two (or three) texture coordinate generation functions to produce multiple curves, each representing a different surface characteristic.
![]()
One way to use a three-dimensional lookup table is to fill it with RGB values that correspond to, for instance, HSV (Hue, Saturation, Value) values. The H, S, and V values index the three dimensional tables. By assigning HSV values to the vertices of a polygon linear color interpolation may be carried out in HSV space rather than RGB space. Other color spaces are easily supported.
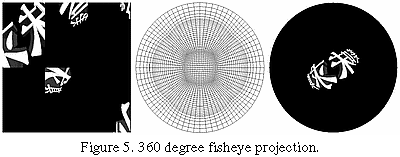
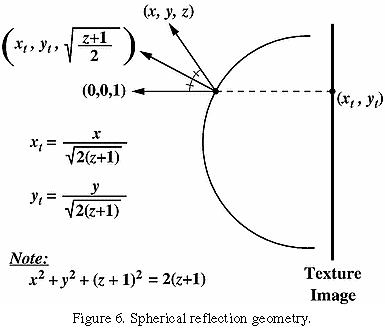
The second method is to generate a single texture image of a perfectly reflecting sphere in the environment. This image consists of a circle representing the hemisphere of the environment behind the viewer, surrounded by an annulus representing the hemisphere in front of the viewer. The image is that of a perfectly reflecting sphere located in the environment when the viewer is infinitely far from the sphere. At each polygon vertex, a texture coordinate generation function generates coordinates that index this texture image, and these are interpolated across the polygon. If the (normalized) reflection vector at a vertex is r = vect(x y z), and m = sqrt(2*(z+1)), then the generated coordinates are x/m and y/m when the texture image is indexed by coordinates ranging from -1 to 1. (The calculation is diagrammed in Figure 6).
![]()
This method has the disadvantage that the texture image must be recomputed whenever the view direction changes, but requires only a single texture image with no special polygon subdivision (Figure 7).
![]()


We hope to have shown that, in addition to its standard uses, texture mapping can be used for a large number of interesting applications, and that texture mapping is a powerful and flexible low level graphics drawing primitive.
[Akeley 93] Kurt Akeley, Personal Communication, 1993
[Bishop 86] G. Bishop and D. M. Weimer, Fast Phong Shading, Computer Graphics (SIGGRAPH '86 Proceedings), Pages 103-106, August, 1986.
[Burns 92] Derrick Burns, Personal Communication, 1992.
[Carey 85] Richard J. Carey and Donald P. Greenberg, Textures for Realistic Image Synthesis, Computer and Graphics, Pages 125-138, Vol. 9, No.3, 1985.
[Catmull 74] Ed Catmull, A Subdivision Algorithm for Computer Display of Curved Surfaces, PhD Thesis, University of Utah, 1974.
[Crow 84] Frank Crow, Summed-Area Tables for Texture Mapping, Computer Graphics (SIGGRAPH '84 Proceedings), Pages 207-212, July, 1984.
[Deering 88] Michael Deering and Stephanie Winner and Bic Schediwy and Chris Duffy and Neil Hunt, The Triangle Processor and Normal Vector Shader: A VLSI System for High Performance Graphics, Computer Graphics (SIGGRAPH '88 Proceedings), Pages 21-30, August, 1988.
[Drebin 88] Robert A. Drebin and Loren Carpenter and Pat Hanrahan, Volume Rendering, Computer Graphics (SIGGRAPH '88 Proceedings), Pages 65-74, August, 1988.
[Drebin 92] Robert A. Drebin, Personal Communication, 1992.
[Gardner 85] Geoffrey. Y. Gardner, Visual Simulation of Clouds, Computer Graphics (SIGGRAPH '85 Proceedings), Pages 297-303, July, 1985.
[Greene 86] Ned Greene, Applications of World Projections, Proceedings of Graphics Interface '86, Pages 108-114, May, 1986.
[Grossman 90] Mark Grossman, Personal Communication, 1990.
[Hanrahan 90] Pat Hanrahan and Jim Lawson, A Language for Shading and Lighting Calculations, Computer Graphics (SIGGRAPH '90 Proceedings), Pages 289-298, August, 1990.
[Heckbert 86] Paul S. Heckbert, Survey of Texture Mapping, IEEE Computer Graphics and Applications, Pages 56-67, November, 1986.
[Heckbert 89] Paul S. Heckbert, Fundamentals of Texture Mapping and Image Warping, M.Sc. Thesis, Department of Electrical Engineering and Computer Science, University of California, Berkeley, June, 1989.
[Laur 91] David Laur and Pat Hanrahan, Hierarchical splatting: A progressive refinement algorithm for volume rendering, Computer Graphics (SIGGRAPH '91 Proceedings), Pages 285-288, July, 1991.
[Oka 87] Masaaki Oka and Kyoya Tsutsui and Akio Ohba and Yoshitaka, Real-Time Manipulation of Texture-Mapped Surfaces, Computer Graphics (SIGGRAPH '87 Proceedings), July, 1987.
[Peachy 85] Darwyn R. Peachey, Solid Texturing of Complex Surfaces, Computer Graphics (SIGGRAPH '85 Proceedings), Pages 279-286, July, 1985.
[Perlin 85] Ken. Perlin, An Image Synthesizer, Computer Graphics (SIGGRAPH '85 Proceedings), Pages 287-296, July, 1985.
[Reeves 87] William Reeves and David Salesin and Rob Cook, Rendering Antialiased Shadows with Depth Maps, Computer Graphics (SIGGRAPH '87 Proceedings), Pages 283-291, July, 1987.
[Sabella 88] Paolo Sabella, A Rendering Algorithm for Visualizing 3D Scalar Fields, Computer Graphics (SIGGRAPH '88 Proceedings), Pages 51-58, August, 1988.
[Saito 90] Takafumi Saito and Tokiichiro Takahashi, Comprehensible Rendering of 3-D Shapes, Computer Graphics (SIGGRAPH '90 Proceedings), Pages 197-206, August, 1990.
[Segal 92] Mark Segal and Carl Korobkin and Rolf van Widenfelt and Jim Foran and Paul Haeberli, Fast Shadows and Lighting Effects using Texture Mapping, Computer Graphics (SIGGRAPH '92 Proceedings), Pages 249-252, July, 1992.
[Westover 90] Lee Westover, Footprint Evaluation for Volume Rendering, Computer Graphics (SIGGRAPH '90 Proceedings), Pages 367-376, August, 1990.
[Whitted 83] Turner Whitted, Anti-Aliased Line Drawing Using Brush Extrusion, Computer Graphics (SIGGRAPH '83 Proceedings), Pages 151-156, July, 1983.
[Williams 83] Lance Williams, Pyramidal Parametrics, Computer Graphics (SIGGRAPH '83 Proceedings), Pages 1-11, July, 1983.