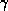In the case of a radio emitting system, an alternate
method to produce x-ray emission is inverse-Compton scattering.
If the relativistic electrons responsible for the radio emission are
produced in proximity to the primary, the photons in the radiation
field of the primary may be inverse-Compton scattered to x-ray
and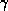 
-ray energies.
For inverse-Compton production, the x-ray and radio emission are both linked to the creation of relativistic particles and one might expect that the x-ray outburst would be very nearly coincident with the radio outburst. The fact that our observations show radio and x-ray outburst peaks at nearly opposite phase contradicts this simple prediction. However, a strict coincidence of radio and x-ray emission is relaxed if the radio and x-ray flux originate from different volumes. To produce detectable, optically-thin radio emission, relativistic particles must either be produced in, or escape to, a region at large radii from the underlying Be star; where they can fill a sufficient volume to be detectable and survive against the high inverse-Compton losses that occur at smaller radii. On the other hand, inverse-Compton x-rays are most efficiently produced close to the star, where the stellar radiation energy density is high.
Paredes et al. (1990) have noted that the phase of peak radio outburst
varies from cycle to cycle, lying within the boundaries 0.4 to 0.9.
In figure 4 we show the distribution of phases of peak radio flux density
along with a schematic of our x-ray light curve.
For clarity the data have been plotted for two cycles.
The open squares indicate the phase and flux density of radio peak for
a complete sample of observed outbursts since the first radio detection
of LSI+61 in 1977.
The phase of peak flux density appears almost uniformly distributed
between phase 0.4 and 1.0. Within this range there is a broad
distribution of peak flux densities up to the maximum
value of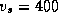 
300 mJy.
The radio periodicity of LSI+61 is defined more by the intervals of no
radio activity than by the active phase.
It is striking that the duration of the high state of the x-ray light
curve matches the range of phases during which the system is, on average,
radio active.
Taylor & Gregory (1984) noted that the radio emission from
LSI+61 is optically-thin during most of the rise of the outburst (as
observed during the second outburst in figure 1) and
consequently there must be continued particle production during at
least the rising portion of the outburst.
The detection, on several occasions, of weaker bursts of emission
past the main outburst (Taylor et al.1992), indicates further
that relativistic particle production continues well past the time of peak
flux density.
The data therefore indicate a continuous period of particle production
during the active radio interval (phase 0.4 - 1.0).
If at least some of this particle production occurs close to the
primary star, a continuous high state of inverse-Compton scattered photons
would be produced during this phase range.
The relative strength and timing of the associated radio activity
from cycle to cycle might then depend on additional factors affecting
the transport of electrons to large radii.
Can we account for the observed luminosity of x-rays in this fashion?
We are developing a model that attempts to
simultaneously fit the radio light curves and
predict the time evolution of emission in high energy photons.
The detailed explanation of the model and the
fits to the light curves will appear in a future paper
(Peracaula et al, 1995). We present here initial calculations
we have done to determine whether sufficient high energy photon luminosity can
be produced by inverse-Compton scattering.
The model consider a cloud of relativistic
particles with spherical symmetry, expanding adiabatically at uniform
velocity and embedded in a magnetic field. The particles are injected
at a constant rate for a finite period of time and with a power-law,
injected energy distribution 
. The relativistic particles
lose energy due to adiabatic expansion, synchrotron radiation
and inverse-Compton scattering.
For a single electron the inverse-Compton losses are given by the
expression:
where 
is the radiation field energy density, given by
Here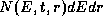 
is the luminosity of the primary and 
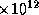is
the distance of the electron from the primary.
To calculate the inverse-Compton losses for a population
of electrons we require the distribution function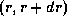 
,
which gives the number of particles at distance
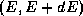from the primary that have an energy 
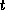at time
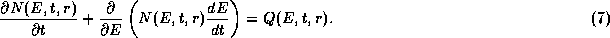. This function is given by the solution to the continuity
equation,
The details of the solution of this equation will be presented by
Peracaula et al. (1995).
The total energy loss rate due to inverse-Compton scattering
as a function of time is given by integrating the quantity
over the volume of the expanding sphere and over the range
of particle energies.
The constraints on this calculation are the observed properties of LSI+61 .
The primary has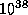 
26,000 K
and luminosity 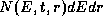about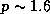 
erg/s (Hutchings & Crampton, 1981).
From analysis of the multi-wavelengths radio observations
(Taylor & Gregory 1984, Paredes et al. 1991)
estimate the power-law index of the energy
distribution for the injected particles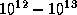 
,
an initial size of 
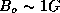cm,
the magnetic field strength at that time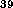 
and a total energy in radio-emitting, relativistic particles of
a few 10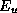
erg.
The inverse-Compton luminosity also depends on the upper energy
limit,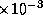 
, of the injected particle distribution function.
To produce scattered
photons with energies above 100 MeV, 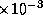must be at least
several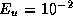 
ergs (see below).
Taking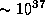 
ergs, and placing the site of particle injection
at a distance equal to the semi-major axis
yields a peak inverse-Compton luminosity of 
erg s
.
This luminosity is sufficient to explain the flux of high energy
photons from LSI+61 above 1 MeV, however it greatly exceeds the x-ray
luminosity.
The low ratio of inverse-Compton x-ray to 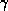-ray luminosity can be
understood as an effect of the expansion of the plasmon of relativistic particles.
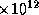A relativistic electron created at a distance from the primary,
will have a lifetime to inverse-Compton scattering of
For an electron to avoid giving up its energy to inverse-Compton
scattering, it must travel outward from the primary with velocity,
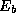(Taylor & Gregory 1982).
This condition defines a break energy, 
, given by:
Electrons with energy greater than have residence times near the
primary longer than the inverse-Compton lifetime, and hence suffer
significant losses. Electron with energy less then escape to
large radii on a time scale shorter than the inverse-Compton lifetime.
This break energy will produce a corresponding low-energy turndown in the
spectrum of inverse-Compton photons. For relativistic particles, the
final energ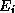y, 
of an inverse-Compton scattered photon is related to
its initial energy,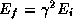 
, as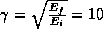 
. At a stellar
temperature of 26,000 K, the peak in the stellar photon distribution
occurs at about 10 eV. The x-ray photons at energies near 1 keV
therefore arises primarily from scattering off electrons with
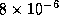, or energies of 
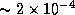erg.
Similarly, 1 MeV
photons are produced by electrons with energies 
erg.
For the observed values of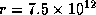 
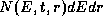and , and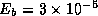 
cm, equation (5) yields a break energy of 
erg
- predicting a spectral turn-down between the MeV and keV range, as
observed.